Hi everyone! Welcome back to another session where we’ll delve into the intriguing world of directed numbers. Today, we’ll focus on something many students find tricky – multiplying and dividing negative numbers. So let’s jump straight into it!
Understanding Multiplication with Negative Numbers
When we multiply negative numbers, it can be a bit confusing. Let’s take a straightforward example:
Imagine we have ( -2 X 3 ).
This means we have three lots of (-2).
Visualising Negative Multiplication
To visualise this:
- We have (-2)
- Another (-2)
- And one more (-2)
So, altogether, we get:
[-2 + -2 + -2 = -6]
Therefore, ( -2 X 3 ) equals ( -6 ). Essentially, we’re just adding (-2) three times.
To reinforce this concept, if we switch the order and write ( 3 X -2 ), the result remains the same. It becomes three lots of (-2):
[3 X -2 = -6]
Multiplication Laws
Remember, multiplication has certain laws. The order of the numbers doesn’t matter; you’ll still get the same product. So, whether it’s ( -2 X 3 ) or ( 3 X -2 ), the answer remains (-6).
Another Example
Let’s consider another example with larger numbers:
[-5 X -4]
This time, we have a negative number multiplied by another negative number. Think of it as ( 5 X 4 ) which equals 20.
However, since we are multiplying two negative numbers, the rule goes that ‘a negative times a negative is a positive’. So, the answer becomes:
[-5 X -4 = 20]
This might seem counterintuitive, but it’s because they cancel each other out to result in a positive number.
“Remember, a negative times a negative results in a positive.”
Division with Negative Numbers
Now, let’s shift our focus to division. Just as with multiplication, division involving negative numbers can be quite straightforward once you grasp the concept.
Division Example
Suppose we have:
[-20 ÷ 4]
We know that 20 divided by 4 is 5. But since we started with a negative number:
[-20 ÷ 4 = -5]
We can visualise this division by thinking about it as distributing 20 negatively into 4 parts.
Similarly, if we had:
[20 ÷ -4]
We’re essentially looking for the negative of ( 20 ÷ 4 ):
[20 ÷ -4 = -5]
Dividing Two Negatives
What if we have to divide two negatives? Consider:
[-20 ÷ -4]
Here, dividing a negative by another negative cancels out the negatives, resulting in a positive number:
[-20 ÷ -4 = 5]
The negative signs neutralise each other, just like in multiplication.
Key Takeaways
To sum up, here are the essential points to remember when dealing with negative numbers:
- Multiplying Two Negatives:
- The result is positive because the negatives cancel each other out.
- Multiplying a Negative with a Positive:
- The result is negative because you’re effectively adding the negative value multiple times.
- Dividing Two Negatives:
- The result is positive, as the negative signs cancel each other out.
- Dividing a Negative by a Positive or Vice Versa:
- The result is negative due to the direction of division.
Practice Problems
For better understanding, try solving these on your own:
- ( -3 X 5 )
- ( -7 X -2 )
- ( 15 ÷ -3 )
- ( -24 ÷ -6 )
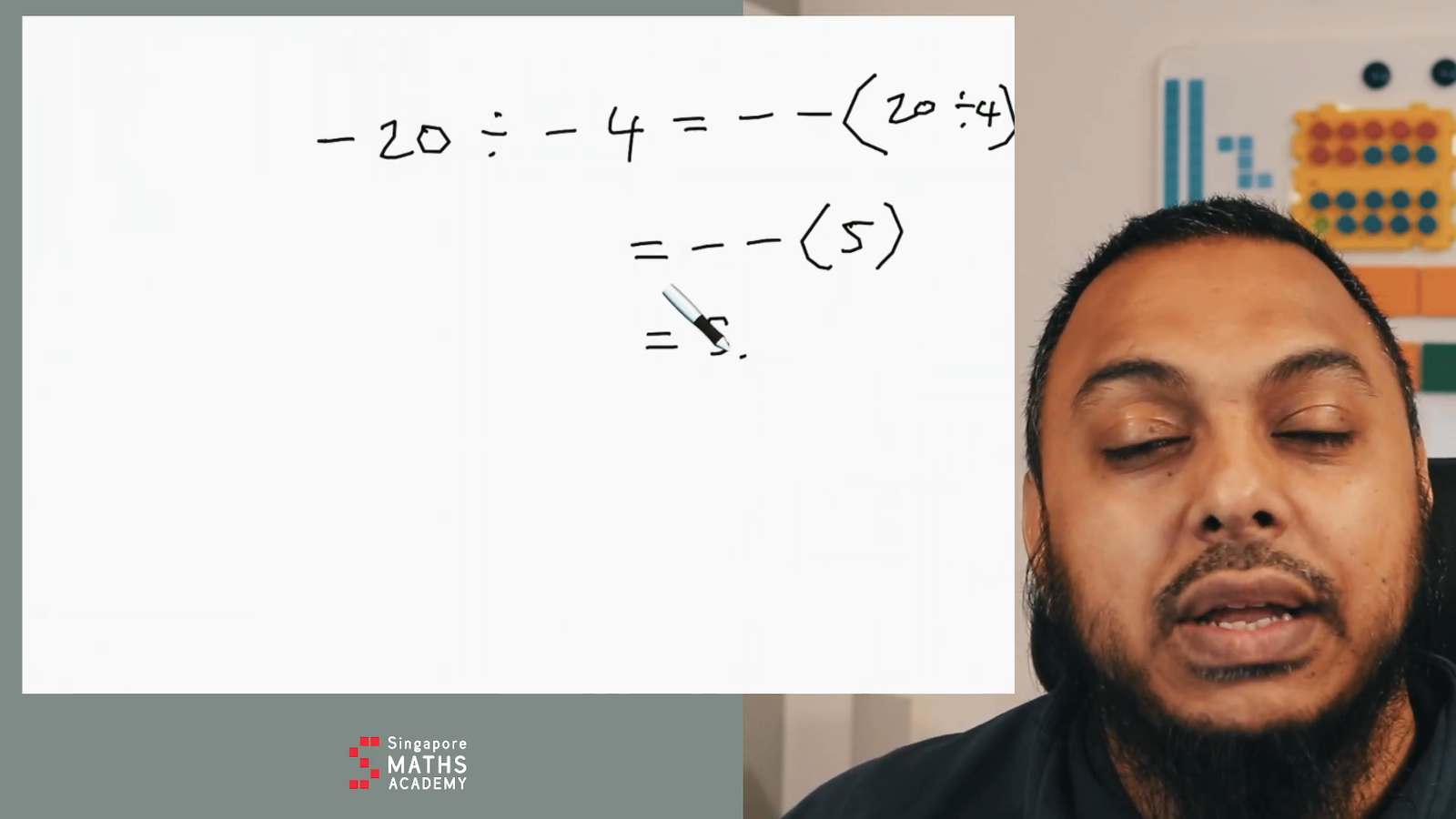
By practising these problems, you’ll enhance your understanding of how negative numbers behave in multiplication and division. With patience and regular practice, you’ll master these concepts in no time!