If you are preparing your child for the 11+ exams (GL, CEM, or CSSE), you have likely encountered a grid of numbers that looks like a Sudoku puzzle but requires a different kind of logic. These are Magic Squares.

While they might look like simple arithmetic drills, Magic Squares are actually one of the oldest mathematical puzzles in human history. Examiners love them because they test two things at once: arithmetic fluency (adding quickly) and logical reasoning (spotting patterns).

To help your child conquer these questions, it helps to understand where they come from and how they work.

The Legend of the Turtle (A Brief History)

The story of the Magic Square begins in Ancient China, around 2200 BC. According to legend, a massive flood was destroying the land. As the Emperor Yu stood on the banks of the River Lo, a turtle emerged from the water.

This was no ordinary turtle. On its shell was a pattern of dots arranged in a 3×3 grid. The Emperor noticed something strange: whether he counted the dots vertically, horizontally, or diagonally, they always added up to the number 15.

This pattern became known as the Lo Shu Square. It was considered mystical for centuries, representing the perfect balance of the universe. Today, that “perfect balance” is exactly what your child needs to demonstrate in their exam.

Level 1: The “Standard” Question

In the 11+ exam, the examiner will usually start gently. They want to see if the student understands the basic definition of a Magic Square: Every row, column, and diagonal sums to the same number.

Here is a recreation of a standard question (Question 1).

Question 1:

What is the missing number in the middle of this magic square?

11+ Magic Squares standard question

How most students solve it:

  1. They scan the grid for a complete line.
  2. They spot the top row: 5 + 4 + 9 = 18.
  3. They now know the Magic Sum is 18.
  4. They look at the middle row: 10 + ? + 2 = 18.
  5. Basic algebra tells them the missing number is 6.

This is the “Arithmetic Approach.” It works, but it’s slow, and it relies on the examiner giving you an “easy” row.

Level 2: The “Killer” Question

To separate the top 10% of students, examiners will provide a grid without a complete row. This removes the ability to simply “add up” and forces the student to rely on the mathematical properties of the square.

Look at Question 11. This is where students panic.

Question 11:

The diagram shows part of a magic square. What is the value of m?

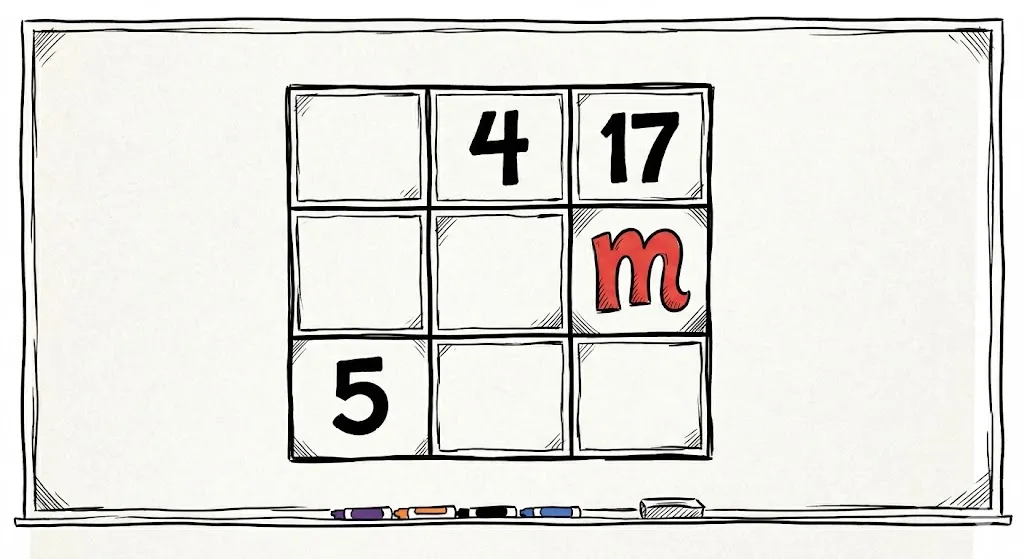
11+ Magic Squares challenging question

Why this is hard: There is no full row. There is no full column. There is no full diagonal. If your child tries to find the Magic Sum by adding, they will hit a dead end.

To solve this, you need to understand the fundamentals AND have strong algebra skills.

The Fundamental Tip: The “Middle Number” Secret

If you understand how Magic Squares are built, you don’t always need to do difficult addition.

Tip #1: The Middle Numbers Reveal the Sum Most 11+ Magic Square questions use a sequence of numbers (like 1–9) or a pattern (like even numbers).

If you write the numbers out in order, the Middle Three Numbers tell you everything you need to know.

  1. Write the numbers in order.
  2. Circle the middle three.
  3. Add them up.

If the numbers were 1 to 9: 1, 2, 3, (4, 5, 6), 7, 8, 9

4 + 5 + 6 = 15. The Magic Sum is 15. The center number of the grid is usually the middle number of the sequence (5).

By knowing these rules, a student can look at a seemingly impossible question like #11 and start applying logic rather than guesswork.

Ready to Master the Logic?

We have built an interactive Magic Numbers Challenge designed specifically to take students from “Apprentice” to “Grandmaster.”

It trains the brain to spot these patterns instantly, turning a 5-minute struggle into a 30-second win.