Hi everyone. Welcome back to another eleven-plus journey video. This is Mohhi Dina Ahmed from Singapore Maths Academy. Today we’re diving into another percentage question – a challenging reverse percentage problem that many children often get stuck on or misunderstand, leading to mistakes.
So, let’s jump onto my iPad and work through this question together.
Understanding the Problem
The problem we’re looking at states:
In a sale, prices were reduced by 35%. The sale price of a computer was £884. Work out the normal price of the computer.
Visualising the Problem with a Bar Model
To understand and solve the problem, let’s represent it with a bar model. This helps us visualise the normal and sale prices more clearly.
Step 1: Represent the Normal Price
Firstly, we consider the normal price as 100%.
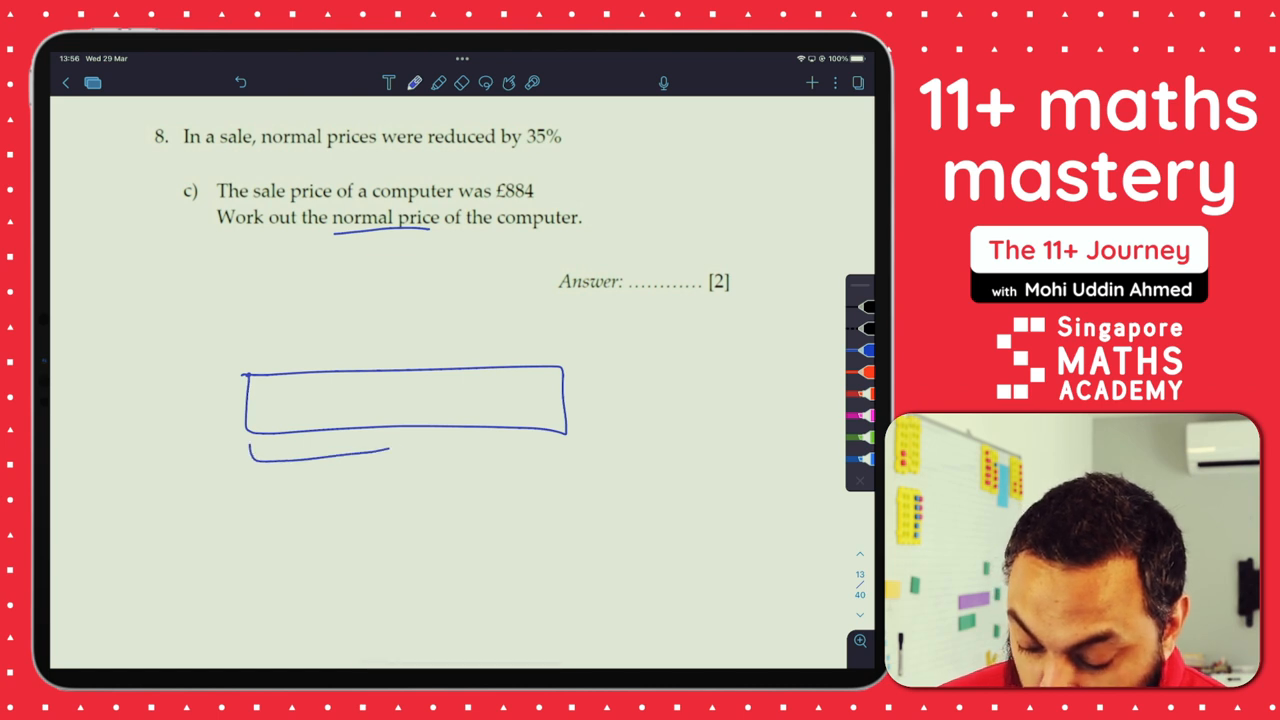
In this bar model, the entire length represents 100% of the normal price.
Step 2: Show the Reduction
The price reduction is 35%. By removing 35% from the bar, we can indicate this reduction visually.
What we have left in our bar model represents the sale price.
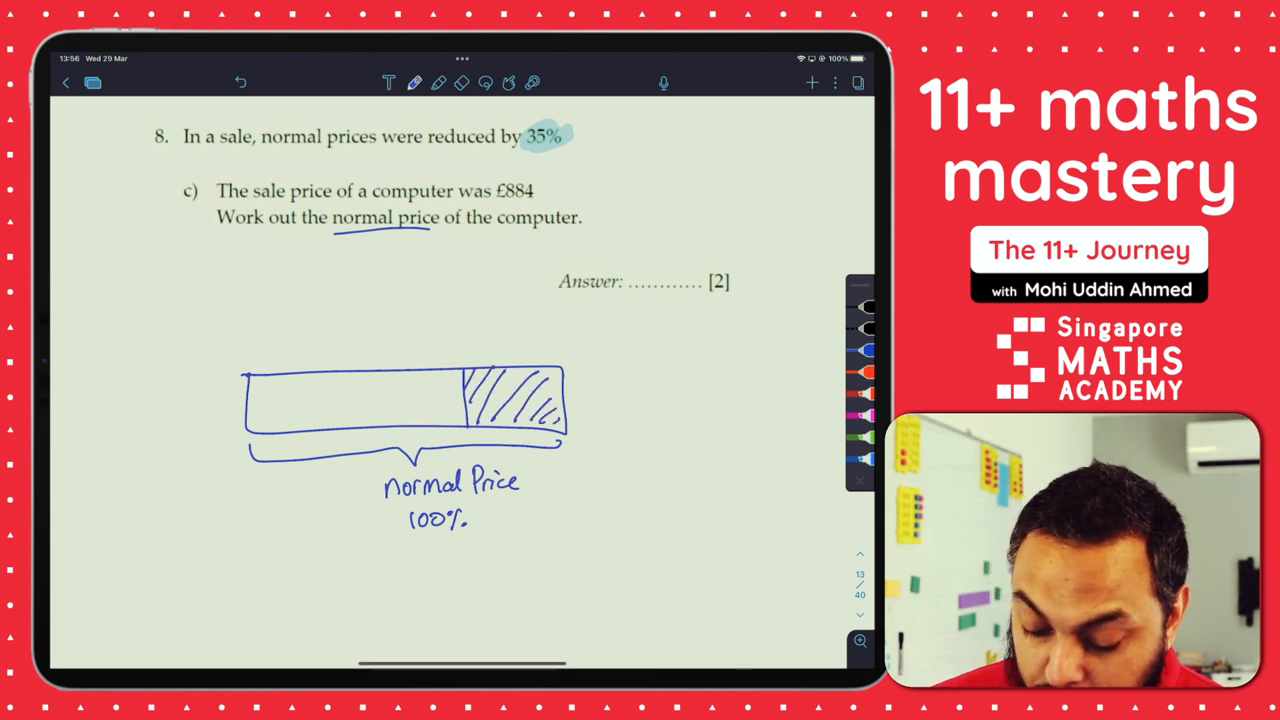
Step 3: Determine the Sale Price Percentage
The sale price remains as a portion of the normal price. Specifically:
- Normal Price = 100%
- Reduced by = 35%
- Sale Price = 100% – 35% = 65%
So, the sale price is 65% of the original price.
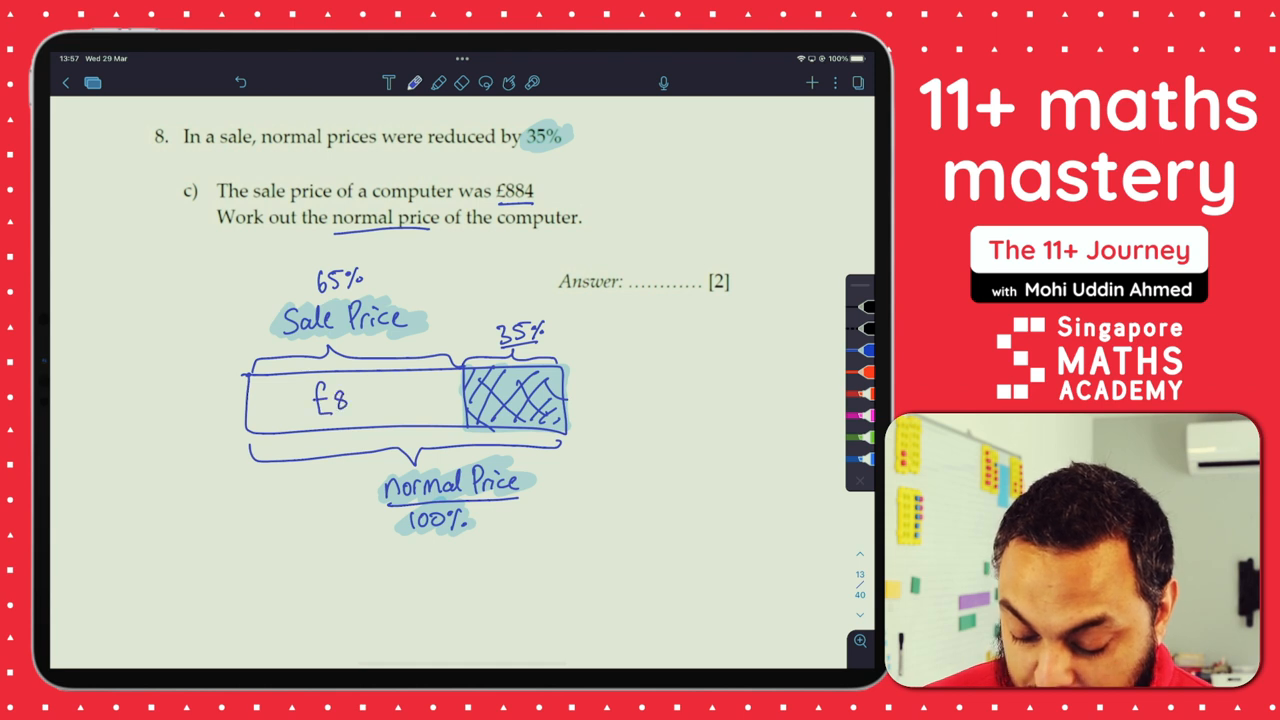
Solving the Reverse Percentage Problem
Given that the sale price is 65% of the normal price and the actual sale price is £884, let’s find the original normal price.
Step 1: Set Up the Equation
65% of the normal price equals £884.
Step 2: Find 1%
To find the normal price, we first need to determine what 1% of the normal price would be.
We calculate:
[ 65% of Normal Price = £884 ]
[ 1% of Normal Price =£884/ 65 ]
Step 3: Simplify the Calculation
Dividing by 65 can be tricky, so let’s look for an easier breakdown.
Potential approaches:
- Divide by 5: [ {884}{5} = 176.8 ]
- Divide by 13: [ {£884}{13} = 68 ]
By choosing the second method:
[ 884 \div 13 = 68 \ (\text{This represents 5% of the normal price}) ]
Step 4: Calculate 100%
If 5% is £68, then:
[ 10% = £68 \times 2 = £136 ]
[ 100% = £136 \times 10 = £1,360 ]
Thus, the normal price of the computer is £1,360.
Common Mistakes and Tips
Mistakes to Avoid
A common mistake students make is misinterpreting the percentage. They calculate 35% of the sale price (£884) and then add it to £884
This leads to a wrong answer. Remember:
“The sale price is 65% of the original price, not the other way round.”
Practice Makes Perfect
To avoid such mistakes, practice reverse percentage problems frequently. Search for “reverse percentage worksheets” online for more exercises.
Conclusion
I hope this explanation helps clarify how to tackle reverse percentage problems. If you have any questions or need further clarification, leave a comment below. If you found this helpful, please give a thumbs up or subscribe to our YouTube channel.
For additional tuition needs, feel free to contact us through Facebook or Instagram. We’d love to hear from you!
Take care, everyone!

