In this blog post, we’ll dive into the final question of the Merchant Taylors’ School specimen paper. This problem involves calculating the number of bounces a ball will make before its height reduces to less than 25% of its original height. Let’s break down the problem step by step and make sure we understand every part of the calculation.
The Problem Statement
A ball is dropped and bounces up to a height that is 75% of the height from which it was dropped. It then bounces again to a height that is 75% of the previous height, and so on. How many bounces does it make before it bounces to a height that is less than 25% of the original height?
First, let’s summarise the critical details of the problem:
- The ball’s bouncing height is 75% of the previous height.
- We need to determine how many bounces occur before the ball’s height is less than 25% of the original height.
Visualising the Bounces
To better understand the problem, let’s visualise it:
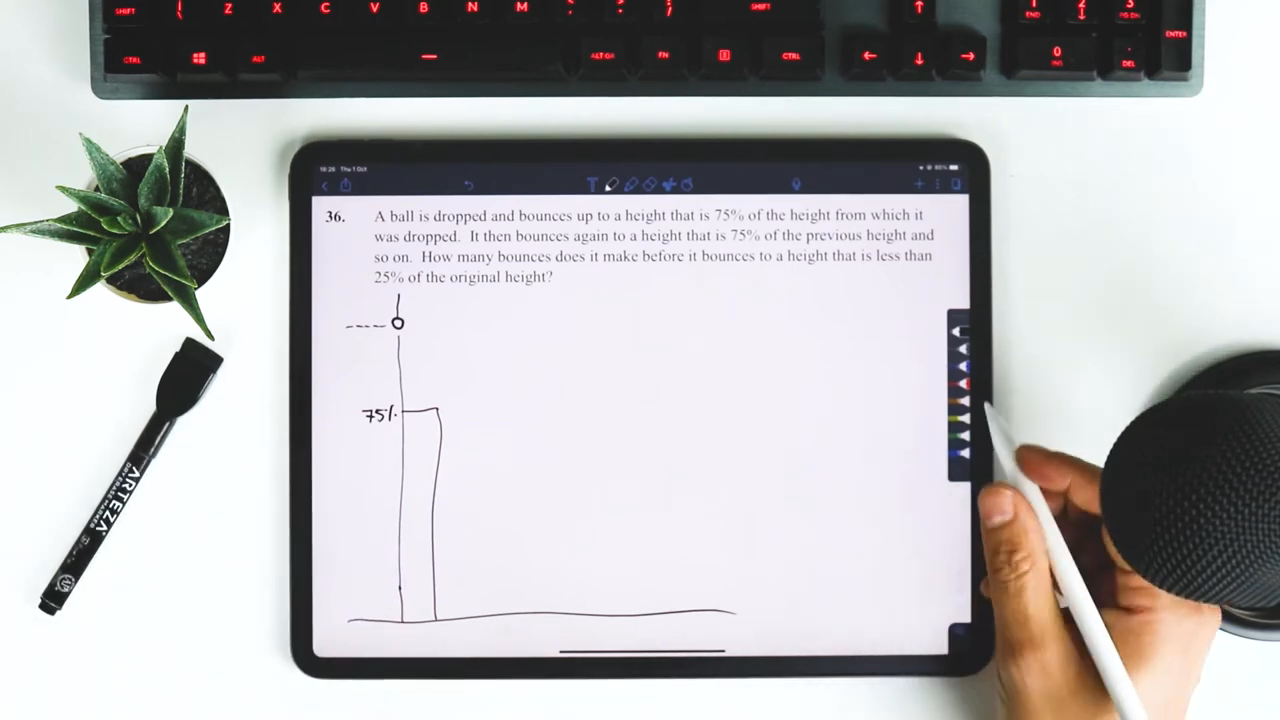
Imagine our ball starting at a certain height, and each time it bounces, it reaches a new height that’s 75% of the height from which it was dropped.
Key Points:
- The first height is the original height.
- Each consecutive height reduces to 75% of the previous height.
- We need to find out after how many bounces the height is less than 25% of the original height.
Calculating the Heights Step by Step
Initial Height
We start with the original height, let’s call it H.
First Bounce
After the first bounce, the height is:[ 0.75 \times H ]
Second Bounce
The second height would be:[ 0.75 \times (0.75 \times H) ][ 0.75^2 \times H ][ \frac{3}{4} \times \frac{3}{4} \times H ][ \frac{9}{16} \times H ]
Third Bounce
Following the same pattern:[ 0.75 \times (\frac{9}{16} \times H) ][ 0.75^3 \times H ][ \frac{27}{64} \times H ]
Continuing This Pattern
Continuing this pattern, the height after ( n ) bounces is:[ (0.75)^n \times H ][ \left(\frac{3}{4}\right)^n \times H ]
Setting Up the Inequality
We need to find when this height is less than 25% of the original height:[ (0.75)^n \times H < 0.25 \times H ]
Removing ( H ) from both sides as it is positive and non-zero:[ (0.75)^n < 0.25 ]
To solve this, it can be helpful to take the logarithm of both sides. But first, let’s estimate the value visually before diving deep.
Visual Prompt:[ (0.75)^1 = 0.75 ][ (0.75)^2 = 0.5625 ][ (0.75)^3 = 0.421875 ][ (0.75)^4 = 0.31640625 ][ (0.75)^5 = 0.2373046875 ]
At the fifth bounce:[ (0.75)^5 \approx 0.2373 ]
Since 0.2373 is less than 0.25, we identify that after the fifth bounce, the height is indeed less than 25% of the original height.
Breaking Down the Calculation
To ensure accuracy, let’s delve into the mathematical steps more deeply:
Step 1: Understand the Repetitive Multiplication
Each bounce reduces the height to 75% of its former height, which can be mathematically represented as repeated multiplication of the fraction:
Step 2: Work with Fractions
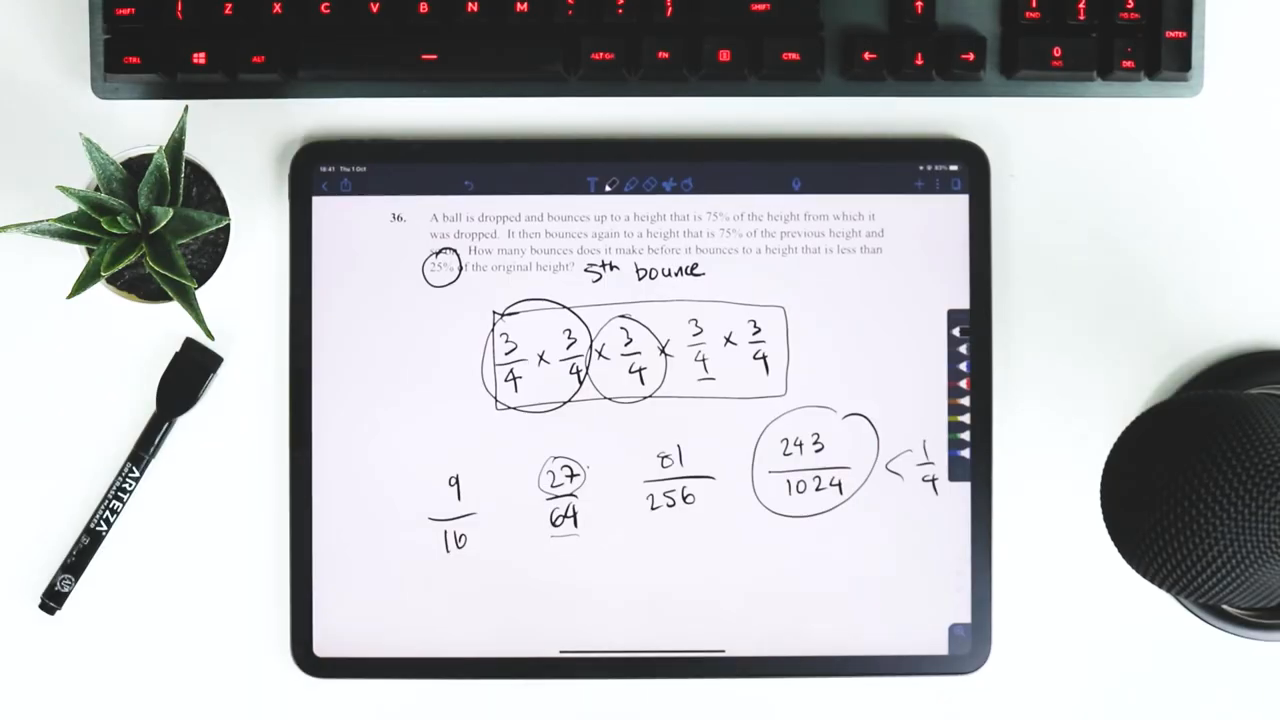
Converting 0.75 into fractions:[ 0.75 = \frac{3}{4} ]This turns our height calculation into:[ \left(\frac{3}{4}\right)^n ]
Step 3: Exponentiation of Fractions
Calculate this iteratively:[ \left(\frac{3}{4}\right)^2 = \frac{9}{16} ][ \left(\frac{3}{4}\right)^3 = \frac{27}{64} ][ \left(\frac{3}{4}\right)^4 = \frac{81}{256} ]
Step 4: Calculating the Fraction
We need:[ \left(\frac{3}{4}\right)^5 = \frac{243}{1024} ]As we calculated earlier:[ 0.2373 < 0.25 ]Therefore, after the 5th bounce, the calculation confirms that the height is indeed less than 25% of the original height.
“On the fifth bounce, the height will be less than 25% of the original height.”
Alternative Simplistic Approach
We also mentioned another approach using percentages which could simplify our thought process.
Using Percentages for Calculation
Instead of fractions:
- The first bounce: 75% of the original height
- The second bounce: (0.75 \times 0.75 = 56.25%)
- The third bounce: (0.75 \times 56.25% = 42.1875%)
- The fourth bounce: (0.75 \times 42.1875% = 31.64%)
- The fifth bounce: (0.75 \times 31.64% = 23.73%)
Converting these percentages into figures:
- 1st bounce: 75%
- 2nd bounce: 56.25%
- 3rd bounce: 42.1875%
- 4th bounce: 31.64%
- 5th bounce: 23.73%
Again, after five bounces, it reaches below 25%.
Conclusion
In conclusion, by either fractional or percentage calculation, we found that:
On the fifth bounce, the ball’s height will be less than 25% of its original height.
This problem reinforces the concept of exponential decay and iterative multiplication within a real-world context. Practice these steps to become more comfortable with handling percentage reductions and fractions systematically.
Happy learning and keep practising—each bounce of learning takes you closer to mastering concepts!